图 7是行星角动量L=2*pi*(1^2)时，有效势能随离太阳距离r的变化曲线，图中顶上一条是行星的离心势能曲线，底下一条是行星的引力势能曲线，中间便是上述两条曲线合成的所谓有效势能曲线，正是这条曲线决定了行星绕日运行的轨道形状。请结合图6和图7，找出行星运动有效势能最大值与其运行轨道的关系，并通过修改上述程序计算验证。
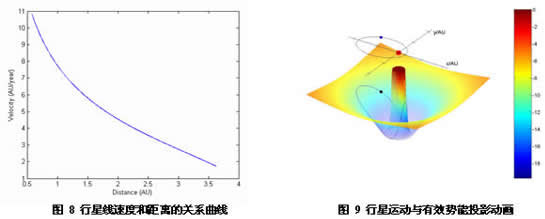
    上面已经验证，行星在运动过程中满足角动量守恒，这使行星运行速度随半径r的变化而变化。图 8 是在角动量L=2*pi*(1^2)，r0=0.58AU时，行星在椭圆轨道各处的速度与r的关系，显然，行星在近日点的速度要大于远日点。在程序后加入以下一段语句，我们可以通过动画的形式更加形象的展示行星运动的各种特征。

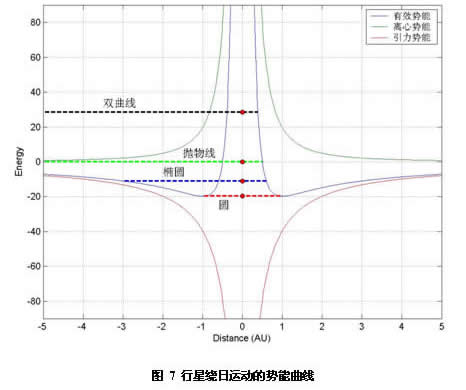
    图 9 所示的是在角动量L=2*pi*(1^2)，r0=0.58AU时，行星运行的动画，轨道下方是行星在有效势能面上的投影。通过动画可以看到行星在运动过程中速度大小的周期性变化(注 )，同时还能形象的观察到行星有效势能的变化。通过改变初始位置，可以得到不同形状的运行轨道，从中可进一步理解行星有效势能对其运行轨道的影响。