在计算运动轨道的循环过程中，需要建立一些矩阵来存放每一步计算得到的位置、速度、动能和势能等物理量。由于在这里我们只重视行星机械能的变化情况，所以为了计算方便把其质量设置为1。具体的程序如下：
   
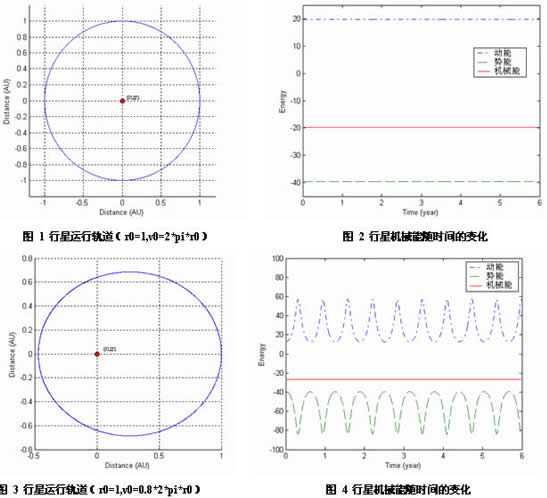
    图 1是6个周期内行星的运动轨迹，其初始位置r0=1AU，初始速度v0=2pir0，时间步长取0.001year。图 2给出了相应的动能、势能和总机械能的变化情况。从中我们可以看到，行星能在一个稳定的轨道上运动，而且其机械能始终保持不变。由于行星的动能和势能也保持稳定，我们能判断行星在这种初始条件下的运行轨道是一严格的圆形（见3.2.4节内容）。
    通过改变初始速度的大小，我们可以得到其他形状的轨道。例如，当我们取r0=1AU, v0=0.8*2pir0时，我们得到了椭圆运行轨道。图 3和图 4计算得到了6year内的行星运动轨道和相应能量随时间的变化，时间步长取0.001year。从图中可以看到，在这种情况下，行星的运行轨道仍是稳定的，它的动能和势能随时间呈周期性变化，但总的机械能保持不变，仔细观察还能发现，这时行星绕太阳运动的周期已经不再是1year了。