最后，我们通过一个动画来形象直观的看一下气体分子的分布状态与系统熵的关系。图9为动画过程中截取的一幅画面。
　　在这个过程中，你体会到熵和孤立系统无序度的关系了吗？


　　1.7 思考与练习

　　1)当用计算机模拟随机行走时，采取不同的随机走法可能会获得不同的答案。下面给出另外两种随机行走的方法，请修改程序，用以下随机走法模拟气体分子的扩散，并对结果进行比较。
　　①在[-1，1]范围随机选择和，在这种方式中，每个方向上正和负的步数大致相等。
　　②在[-1，1]间选择随机值和

　　2)请修改程序，模拟三维空间中气体分子的扩散运动，并计算其熵随时间的变化。
　　3)如图10所示，矩形的盒子被一档板等体积的分成两部分，气体分子先在左边的区域有一点扩散开来，达到稳定后把挡板抽去，气体分子会扩散到右边区域。请通过修改程序模拟这一过程，并计算熵随时间的变化。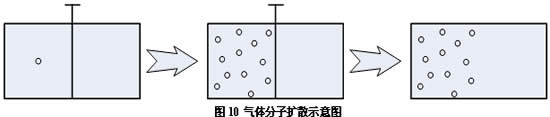

　　4)编写程序实现以下问题：设有N枚硬币，开始时所有的硬币都是分值向上，接着随机的选取硬币并随机的决定是否把其翻转，经过一段时间后，统计分值向上或是国徽向上的硬币所占的比例，并计算在这个系统中熵随计算步数的变化。

　　5)参阅本节附录内容，了解蒙特卡罗积分的原理，编写程序求出10维积分:
　,检验你的数值解答，与解析值155/6比较。