为了让这些分子动起来，我们需要给出运动的方向和步长。这里我们选择步长三ss=1，并在极坐标下通过随机数产生函数给出分子随机的运动方向，之后再回到笛卡儿坐标系中换算出每个分子位置的x、y分量。相应的Matlab程序段如下：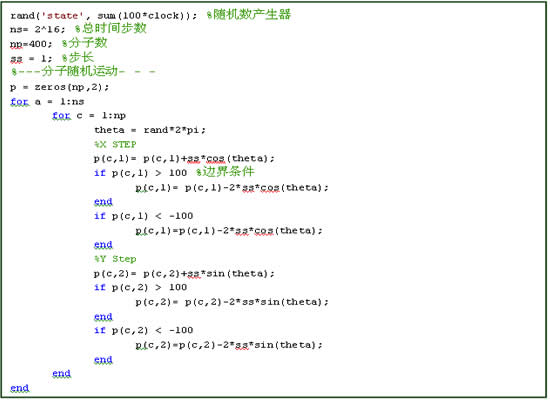

　　在程序中可以看到，我们设置了每个方向上-100~100的边界，当分子遇到边界时会发生弹性碰撞。现在我们就建立了一个有400个分子在二维平面内的扩散模型，但是在作进一步模拟之前，我们要对其准确性做一些基本的测试。

    1.4 对随机数的测试
    为了检测上述随机行走程序是否准确，我们要进行一个简单的测试。假设所有的分子最初都在原点位置，那么经过一步计算以后，原点应该不再有分子，如果我们使用的随机数很好的话，就应该能得到各个方向均匀分布的分子，它们形成一个以原点为圆心，半径为1的圆环。
    如图1所示，我们得到了圆环状、半径为一的粒子分布图，400个分子在圆环上的分布也是很均匀，这说明我们的随机数是可行的。